Что такое МАТЛАБ
MATLAB — это среда программирования высокого уровня, разработанная MathWorks. Он широко используется в научных и инженерных областях для численных вычислений, анализа данных и визуализации. MATLAB предоставляет обширный набор встроенных функций и наборов инструментов, которые делают его лучшей платформой для работы с данными.
Важность построения
Построение данных играет решающую роль в анализе и визуализации данных. Создавая графики, мы можем визуально представлять сложные наборы данных, выявлять закономерности, тенденции и выбросы, а также эффективно передавать информацию. MATLAB предлагает полный набор функций построения графиков, которые позволяют нам создавать визуально привлекательные и информативные графики.
Базовое построение графиков в MATLAB
В этом разделе будут рассмотрены некоторые основные шаги построения графика в MATLAB, это может быть либо график простых точек данных, либо ряд точек данных.
Создание фигуры
В MATLAB фигура — это окно или контейнер, который содержит один или несколько графиков. фигура Команда создаст новую фигуру в окне. Вот пример:
фигура;
Эта команда открывает пустое окно рисунка, где вы можете добавить свои графики.
Добавление осей
Оси - это отдельные графики внутри фигуры. Чтобы добавить оси к фигуре, вы можете использовать функцию, называемую оси . Вот пример:
оси;По умолчанию MATLAB автоматически позиционирует оси так, чтобы они занимали все окно фигуры. Мы также можем настроить размер и положение осей.
Отображение данных
После создания новой фигуры и определения осей мы можем двигаться дальше, нанося различные точки данных. MATLAB предоставляет несколько функций для различных типов графиков, таких как графики для двухмерных линейных графиков, точечные графики для точечных графиков и столбцы для гистограмм.
Следующие команды используют функцию графика MATLAB для отображения точек на фигуре:
Икс '=' 1 : 10 ;и '=' х.^ 2 ;
сюжет ( Икс , и ) ;
Этот код отображает точки (1,1), (2,4), (3,9) и т. д., создавая простую параболическую кривую.
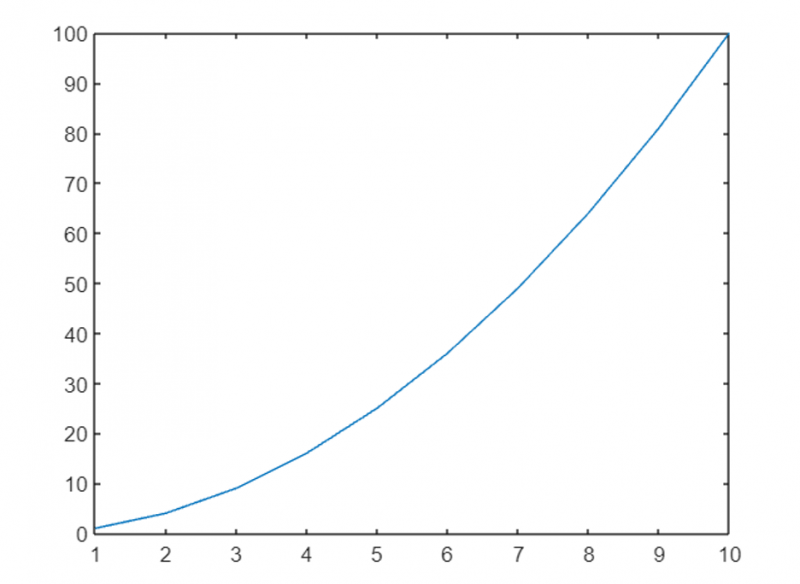
Настройка графиков
MATLAB позволяет нам настраивать различные аспекты графиков, чтобы сделать их более визуально привлекательными и значимыми. Давайте рассмотрим некоторые общие параметры настройки:
Стили и цвета линий
Мы можем настроить внешний вид сюжетных линий, указав различные стили и цвета линий.
Например , мы можем использовать символ «-» для сплошной линии, «-» для пунктирной линии, «:» для пунктирной линии и «-.» для штрихпунктирной линии. Кроме того, вы можете указать цвета, используя предопределенные имена или значения RGB.
Икс '=' 1 : 10 ;у1 '=' х.^ 2 ;
у2 '=' х.^ 3 ;
сюжет ( Икс , у1 , '-р' ) ; % Красная сплошная линия
подожди ;
сюжет ( Икс , у2 , '--б' ) ; % Синяя пунктирная линия
откладывать ;
Приведенные выше команды будут отображать две разные кривые, содержащие разные стили линий и уникальные цвета. Обе команды удержания обеспечат построение обеих кривых на одном рисунке.
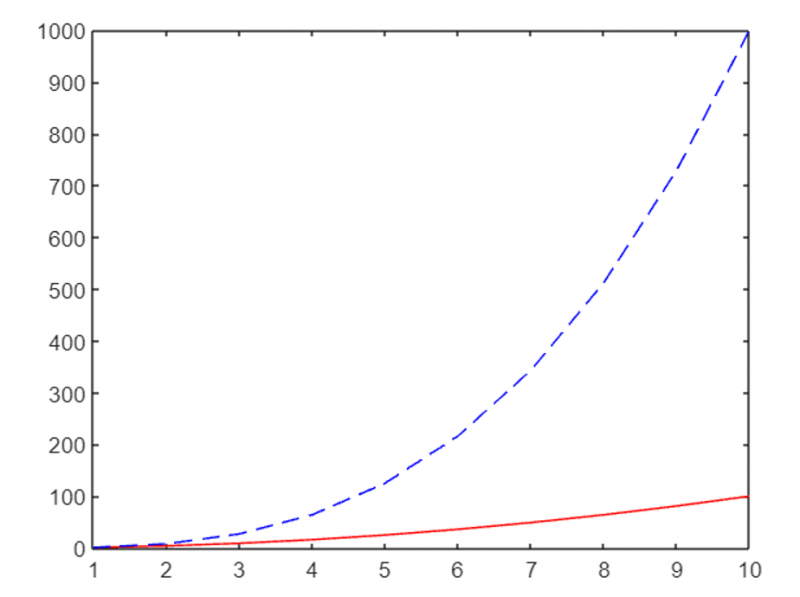
Добавление заголовков и меток
Чтобы сделать графики более информативными, мы можем добавить названия и метки к осям. MATLAB предоставляет такие функции, как заголовок , xметка , и ylabel для этой цели.
Вот пример:
Икс '=' 1 : 10 ;и '=' х.^ 2 ;
сюжет ( Икс , и ) ;
заголовок ( «Сюжет х ^ 2» ) ;
xметка ( 'Икс' ) ;
ylabel ( 'и' ) ;
Используя эти функции, мы добавляем заголовок к графику и соответственно помечаем оси x и y.
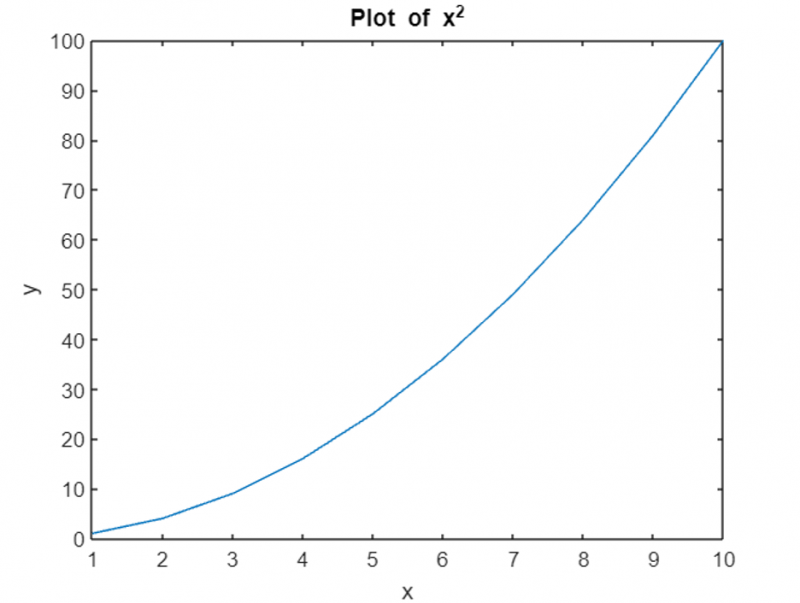
Регулировка осей
Иногда пределы осей по умолчанию и деления могут не подходить для данных. MATLAB позволяет нам настраивать диапазон осей и деления, используя такие функции, как xlim , начальство , xticks , и тики .
Рассмотрим следующий пример:
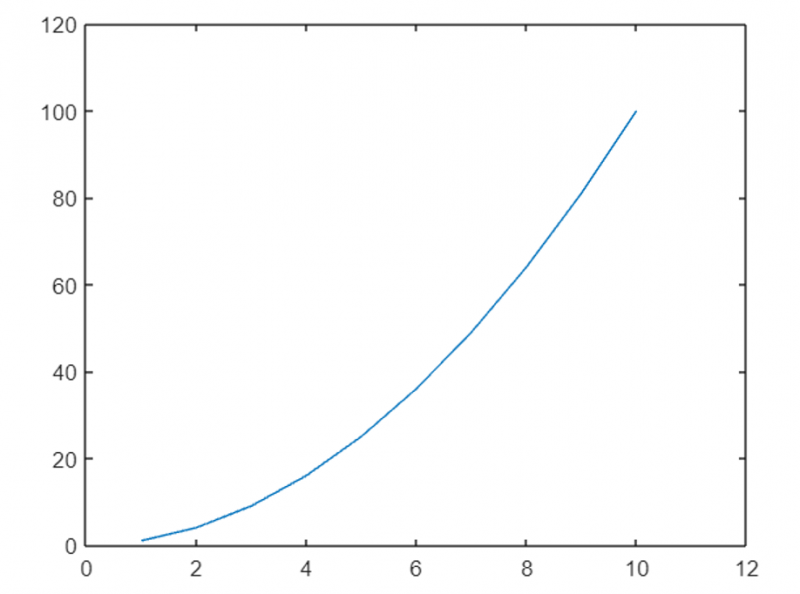
Икс '=' 1 : 10 ;и '=' х.^ 2 ;
сюжет ( Икс , и ) ;
xlim ( [ 0 , 12 ] ) ; % Установить ограничения по оси x
начальство ( [ 0 , 120 ] ) ; % Установить ограничения по оси Y
xticks ( 0 : 2 : 12 ) ; % Установка делений по оси X
тики ( 0 : двадцать : 120 ) ; % Установка делений по оси Y
В этом коде мы настраиваем пределы осей и указываем деления для обеих осей.
Расширенные методы построения графиков
Подсюжеты
В MATLAB подграфики позволяют нам создавать несколько графиков на одной фигуре. Подграфики позволяют нам визуализировать и сравнивать несколько наборов данных одновременно. Эта функция делит фигуры на подграфики.
Вот пример:
Икс '=' 1 : 10 ;у1 '=' х.^ 2 ;
у2 '=' х.^ 3 ;
подсюжет ( 1 , 2 , 1 ) ; % Создайте сетку 1x2 подграфиков , выбирать первый сюжет
сюжет ( Икс , у1 ) ;
заголовок ( «Сюжет х ^ 2» ) ;
подсюжет ( 1 , 2 , 2 ) ; % Выберите второй участок
сюжет ( Икс , у2 ) ;
заголовок ( «Сюжет х ^ 3» ) ;
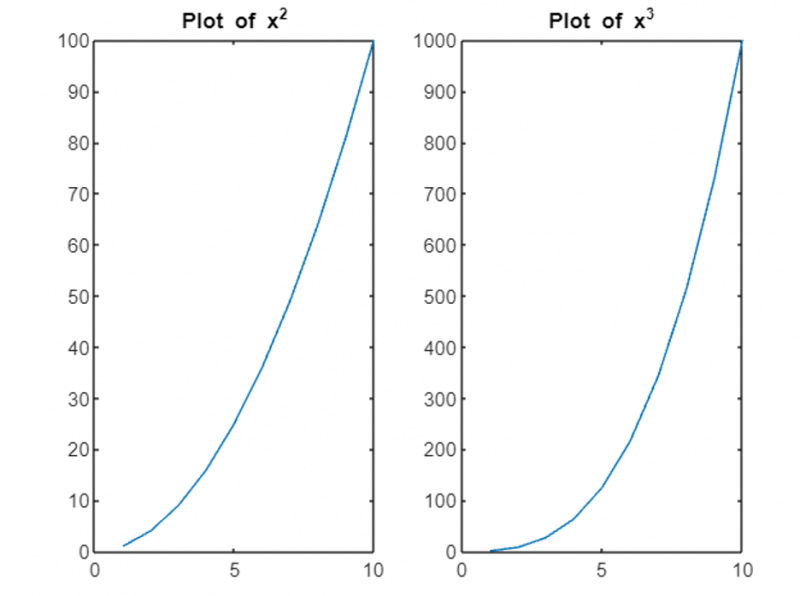
В этом примере мы создаем фигуру с двумя подграфиками, каждая из которых отображает свою кривую.
Несколько графиков на одном рисунке
Помимо подзаголовков, мы также можем добавить несколько графиков на одну фигуру, используя команду удержания. Это позволяет нам накладывать разные графики друг на друга. Рассмотрим следующий пример:
Икс '=' 1 : 10 ;у1 '=' х.^ 2 ;
у2 '=' х.^ 3 ;
сюжет ( Икс , у1 ) ;
подожди ;
сюжет ( Икс , у2 ) ;
откладывать ;
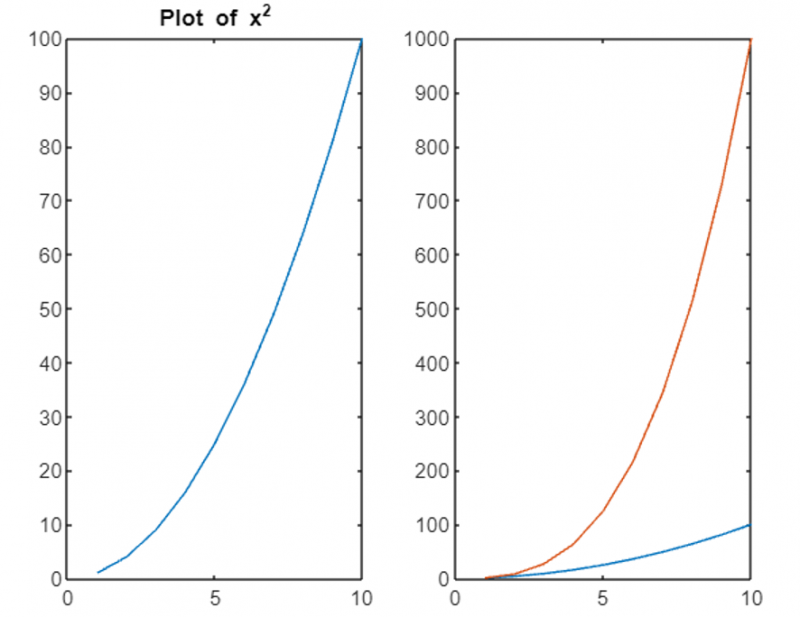
Здесь обе кривые нанесены на один и тот же рисунок, что обеспечивает визуальное сравнение.
3D-графики
В дополнение к 2D-графикам MATLAB предлагает мощные возможности для создания 3D-графиков. Эти графики помогают визуализировать данные в трех измерениях, добавляя глубину визуализации. Функция plot3 создает трехмерные графики.
Рассмотрим следующий пример:
т '=' линспейс ( 0 , 10 *Пи , 100 ) ;Икс '=' потому что ( т ) ;
и '=' без ( т ) ;
С '=' т ;
сюжет3 ( Икс , и , С ) ;
заголовок ( «3D-сюжет» ) ;
xметка ( 'Икс' ) ;
ylabel ( 'и' ) ;
Злейбл ( 'С' ) ;
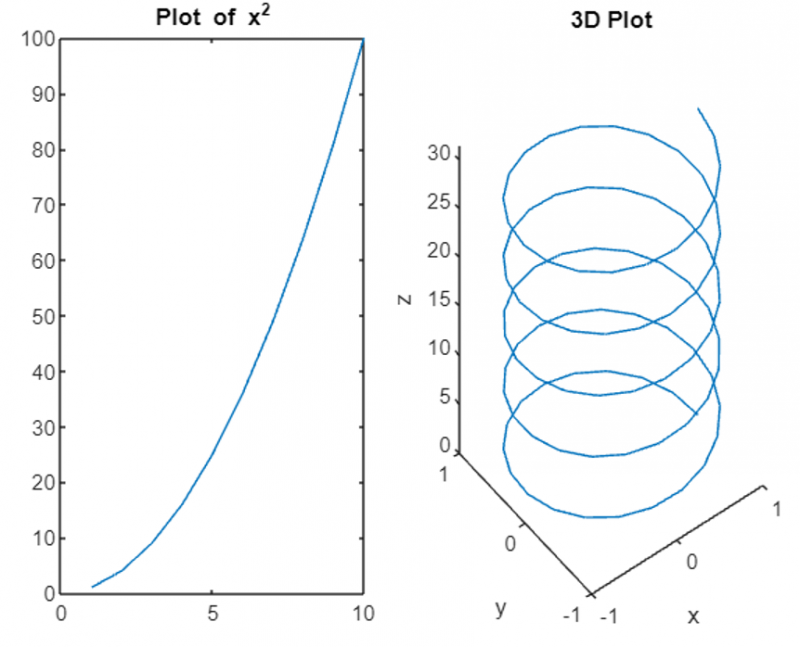
В этом коде мы создаем трехмерный график, указав координаты x, y и z. Полученный график представляет собой спираль в трехмерном пространстве.
Контурные графики
Контурные графики полезны для визуализации трехмерных данных на двумерной плоскости. MATLAB предоставляет функции контура для создания контурных графиков.
Вот пример:
Икс '=' линспейс ( - 2 , 2 , 100 ) ;и '=' линспейс ( - 2 , 2 , 100 ) ;
[ Икс , И ] '=' сетка ( Икс , и ) ;
С '=' Х.^ 2 +Ю.^ 2 ;
контур ( Икс , И , С ) ;
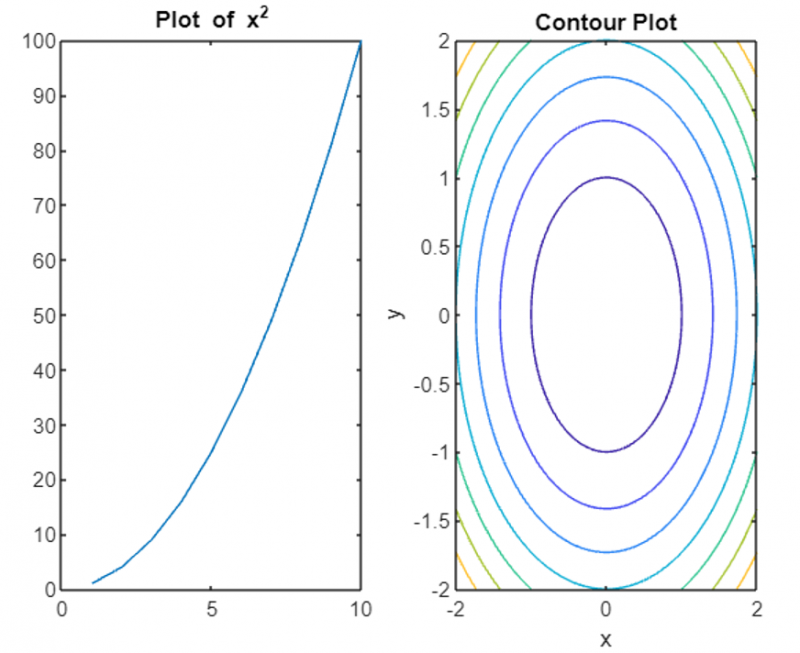
заголовок ( «Контурный участок» ) ;
xметка ( 'Икс' ) ;
ylabel ( 'и' ) ;
В этом примере мы создаем контурный график функции z = x^2 + y^2. Результирующий график показывает контурные линии, которые представляют значения функции.
Заключение
MATLAB предоставляет способы построения точек данных и создания информативных визуализаций. Следуя шагам, описанным в этой статье, мы можем эффективно наносить точки, настраивать графики и изучать передовые методы, такие как подграфики, трехмерные графики и контурные графики. Прочтите приведенную выше статью, чтобы узнать о построении графиков в MATLAB. Это поможет вам визуально анализировать данные и создавать соответствующие выходные данные.