Найти нормальное распределение набора данных — непростая задача; однако мы можем выполнить это в MATLAB, используя команду fitdist() функция. Прочтите это руководство, чтобы подробно узнать о работе с нормальное распределение в MATLAB, используя fitdist() функция.
Что такое нормальное распределение
А нормальное распределение также называемое распределением Гаусса, определяется с использованием двух параметров; среднее и стандартное отклонение точек данных. Среднее значение измеряет среднее значение данных, а стандартное отклонение измеряет, как значения данных распределяются вокруг среднего значения. Используя комбинацию среднего и стандартного отклонения, мы можем рассчитать нормальное распределение из следующей формулы:
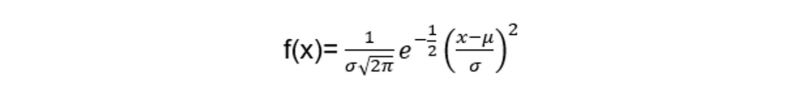
Где:
- Икс представляет значения набора данных.
- е(х) представляет собой функцию вероятности.
- м обозначает
- п обозначает стандартное отклонение.
Как выполнить нормальное распределение в MATLAB Используя функцию fitdist()
MATLAB позволяет нам рассчитать нормальное распределение случайных величин с помощью встроенного fitdist() функция. Эта функция производит нормальное распределение вероятностей объект путем подгонки данного распределения к входным данным. нормальное распределение принимает в качестве входных данных два параметра: стандартное отклонение и среднее значение. Стандартное нормальное распределение имеет нулевое среднее значение, а также единичное стандартное отклонение, равное 1. Это означает, что нормальное распределение центрирован в нуле, а значения распределений равномерно распределены по обе стороны от среднего значения.
Синтаксис
fitdist() в MATLAB можно использовать по-разному:
ПД '=' Fitdist ( Икс , дистальное имя )
ПД '=' Fitdist ( Икс , дистальное имя , Имя , Ценить )
ПДК , гн , гл ] '=' Fitdist ( Икс , дистальное имя , 'К' , групповая переменная )
Здесь:
- Функция pd = fitdist(x,distname) отвечает за подгонку распределения, предоставленного distname, к данным, содержащимся в векторе-столбце x, для создания объекта распределения вероятностей.
- Функция pd = fitdist(x,distname,Name,Value) отвечает за построение объекта распределения вероятностей с одним или несколькими аргументами пары имя-значение, которые определяют дополнительные параметры.
- Функция [pdca,gn,gl] = fitdist(x,distname,’By’,groupvar) отвечает за подгонку распределения вероятностей, определенного distname, к данным в векторе-столбце x на основе группирующей переменной groupvar для создания объектов распределения вероятностей. Он возвращает массив ячеек подобранных объектов распределения вероятностей, обозначаемый как pdca, массив ячеек меток групп, обозначаемый как gn, и массив ячеек уровней группирующих переменных, обозначаемый как gl.
Пример 1. Как найти нормальное распределение с помощью функции fitdist(x,distname)
Этот пример подходит нормальное распределение к выборочным данным z с помощью fitdist() функция.
нагружать пациентовС '=' Масса ;
ПД '=' Fitdist ( С , 'Нормальный' )
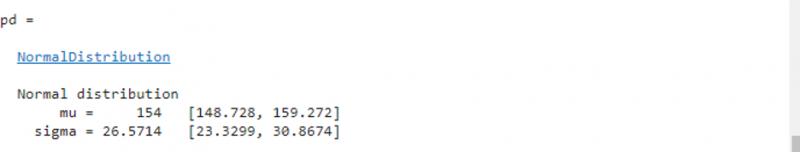
Пример 2. Как найти нормальное распределение с помощью fitdist(x,distname,Name,Value) Функция
В этом примере мы собираемся подогнать распределение ядра к образцу данных, используя fitdist() функция в MATLAB.
нагружать пациентовС '=' Масса ;
ПД '=' Fitdist ( С , «Ядро» , «Ядро» , 'епанечников' )

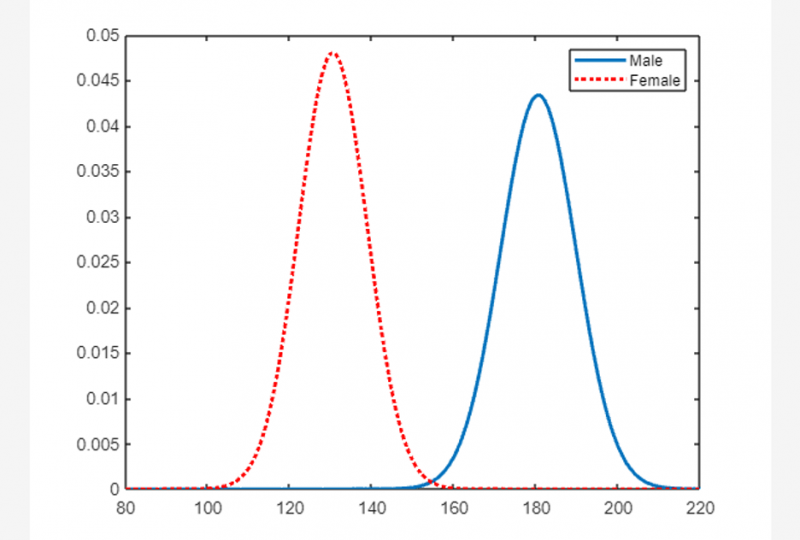
Пример 3. Как найти нормальное распределение с помощью функции fitdist(x,distname,’By’,groupvar)
Приведенный ниже код MATLAB подходит нормальное распределение для сгруппированных данных вычисляет и строит PDF-файл обеих групп данных.
нагружать пациентовС '=' Масса ;
[ ПДК , гн , гл ] '=' Fitdist ( С , 'Нормальный' , 'К' , Пол )
женский '=' ПДК { 1 }
мужской '=' ПДК { 2 }
z_values '=' 80 : 1 : 220 ;
женскийpdf '=' PDF ( женский , z_values ) ;
мужскойpdf '=' PDF ( мужской , z_values ) ;
фигура
сюжет ( z_values , женскийpdf , 'Ширина линии' , 2 )
подожди
сюжет ( z_values , мужскойpdf , 'Цвет' , 'р' , «Стиль линии» , ':' , 'Ширина линии' , 2 )
легенда ( гн , 'Расположение' , 'К северо-востоку' )
откладывать

Заключение
Нахождение нормальное распределение набора данных — это статистический метод, который широко используется в машинном обучении, искусственном интеллекте, науке о данных и многих других областях. Его можно определить с помощью двух параметров; среднее значение, а также стандартное отклонение точек данных. Мы можем поместить набор данных в нормальное распределение объект с помощью fitdist() функция. В этом руководстве представлены основы нормальное распределение функция и как работать с ней в MATLAB, используя fitdist() функция.