Двоичное дерево в C
В С, а бинарное дерево является экземпляром древовидной структуры данных с родительским узлом, который может иметь максимальное количество двух дочерних узлов; 0, 1 или 2 дочерних узла. Каждый отдельный узел в бинарное дерево имеет собственное значение и два указателя на своих дочерних элементов, один указатель на левого дочернего элемента, а другой — на правый дочерний элемент.
Объявление двоичного дерева
А бинарное дерево может быть объявлен в C с использованием объекта с именем структура который изображает один из узлов дерева.
структура узел {
тип данных имя_переменной ;
структура узел * левый ;
структура узел * верно ;
} ;
Выше есть объявление одного бинарное дерево имя узла в качестве узла. Он содержит три значения; одна — это переменная для хранения данных, а две другие — указатели на дочерний элемент. (левый и правый дочерний элемент родительского узла).
Факты о бинарном дереве
Даже для больших наборов данных использование бинарное дерево упрощает и ускоряет поиск. Количество веток дерева не ограничено. В отличие от массива, деревья любого вида можно создавать и увеличивать в зависимости от того, что требуется от человека.
Реализация двоичного дерева в C
Ниже приведено пошаговое руководство по внедрению Бинарное дерево в С.
Шаг 1. Объявите двоичное дерево поиска
Создайте узел структуры с тремя типами данных, такими как данные, *left_child и *right_child, где данные могут быть целочисленного типа, а оба узла *left_child и *right_child могут быть объявлены как NULL или нет.
структура узел{
инт данные ;
структура узел * right_child ;
структура узел * левый_ребенок ;
} ;
Шаг 2: Создайте новые узлы в двоичном дереве поиска
Создайте новый узел, создав функцию, которая принимает целое число в качестве аргумента и предоставляет указатель на новый узел, созданный с этим значением. Используйте функцию malloc() в C для динамического выделения памяти для созданного узла. Инициализируйте левый и правый дочерние элементы значением NULL и верните nodeName.
структура узел * создавать ( данные типа данных )
{
структура узел * имя_узла '=' маллок ( размер ( структура узел ) ) ;
имя_узла -> данные '=' ценить ;
имя_узла -> левый_ребенок '=' имя_узла -> right_child '=' НУЛЕВОЙ ;
возвращаться имя_узла ;
}
Шаг 3: Вставьте правый и левый дочерние элементы в двоичное дерево
Создайте функции insert_left и insert_right, которые будут принимать два входа: значение, которое нужно вставить, и указатель на узел, к которому будут подключены оба потомка. Вызовите функцию создания, чтобы создать новый узел и присвоить возвращенный указатель левому указателю левого дочернего элемента или правому указателю правого дочернего элемента корневого родителя.
структура узел * insert_left ( структура узел * корень , данные типа данных ) {корень -> левый '=' создавать ( данные ) ;
возвращаться корень -> левый ;
}
структура узел * insert_right ( структура узел * корень , данные типа данных ) {
корень -> верно '=' создавать ( данные ) ;
возвращаться корень -> верно ;
}
Шаг 4: Отображение узлов бинарного дерева с использованием методов обхода
Мы можем отображать деревья, используя три метода обхода в C. Вот эти методы обхода:
1: Обход предварительного заказа
В этом методе обхода мы будем проходить узлы в направлении от parent_node->left_child->right_child .
пустота Предварительный заказ ( узел * корень ) {если ( корень ) {
printf ( '%d \n ' , корень -> данные ) ;
display_pre_order ( корень -> левый ) ;
display_pre_order ( корень -> верно ) ;
}
}
2: Обход после заказа
В этом методе обхода мы будем проходить узлы в направлении от левый_дочерний->правый_дочерний->родительский_узел-> .
пустота display_post_order ( узел * корень ) {если ( бинарное_дерево ) {
display_post_order ( корень -> левый ) ;
display_post_order ( корень -> верно ) ;
printf ( '%d \n ' , корень -> данные ) ;
}
}
3: обход по порядку
В этом методе обхода мы будем проходить узлы в направлении от левый_узел-> root_child-> правый_дочерний .
пустота display_in_order ( узел * корень ) {если ( бинарное_дерево ) {
display_in_order ( корень -> левый ) ;
printf ( '%d \n ' , корень -> данные ) ;
display_in_order ( корень -> верно ) ;
}
}
Шаг 5. Выполните удаление в двоичном дереве
Мы можем удалить созданный Бинарное дерево удалив оба дочерних элемента с функцией родительского узла в C следующим образом.
пустота delete_t ( узел * корень ) {если ( корень ) {
delete_t ( корень -> левый ) ;
delete_t ( корень -> верно ) ;
бесплатно ( корень ) ;
}
}
C Программа двоичного дерева поиска
Ниже приведена полная реализация двоичного дерева поиска в программировании на C:
#include#include
структура узел {
инт ценить ;
структура узел * левый , * верно ;
} ;
структура узел * узел1 ( инт данные ) {
структура узел * температура '=' ( структура узел * ) маллок ( размер ( структура узел ) ) ;
температура -> ценить '=' данные ;
температура -> левый '=' температура -> верно '=' НУЛЕВОЙ ;
возвращаться температура ;
}
пустота Распечатать ( структура узел * root_node ) // отображение узлов!
{
если ( root_node '=' НУЛЕВОЙ ) {
Распечатать ( root_node -> левый ) ;
printf ( '%d \n ' , root_node -> ценить ) ;
Распечатать ( root_node -> верно ) ;
}
}
структура узел * вставка_узел ( структура узел * узел , инт данные ) // вставка узлов!
{
если ( узел == НУЛЕВОЙ ) возвращаться узел1 ( данные ) ;
если ( данные < узел -> ценить ) {
узел -> левый '=' вставка_узел ( узел -> левый , данные ) ;
} еще если ( данные > узел -> ценить ) {
узел -> верно '=' вставка_узел ( узел -> верно , данные ) ;
}
возвращаться узел ;
}
инт основной ( ) {
printf ( 'C реализация бинарного дерева поиска! \n \n ' ) ;
структура узел * родитель '=' НУЛЕВОЙ ;
родитель '=' вставка_узел ( родитель , 10 ) ;
вставка_узел ( родитель , 4 ) ;
вставка_узел ( родитель , 66 ) ;
вставка_узел ( родитель , Четыре пять ) ;
вставка_узел ( родитель , 9 ) ;
вставка_узел ( родитель , 7 ) ;
Распечатать ( родитель ) ;
возвращаться 0 ;
}
В приведенном выше коде мы сначала объявляем узел с использованием структура . Затем мы инициализируем новый узел как « узел1 ” и выделять память динамически, используя маллок() в C с данными и двумя указателями типа дочерних элементов, использующих объявленный узел. После этого мы отображаем узел с помощью printf() функцию и вызвать ее в основной() функция. Тогда вставка_узел () создается функция, где если данные узла равны NULL, то узел1 удаляется, в противном случае данные помещаются в узел (родитель) левого и правого потомка. Программа начинает выполнение с основной() Функция, которая создает узел, используя несколько образцов узлов в качестве дочерних, а затем использует методы обхода по порядку для вывода содержимого узла.
Выход
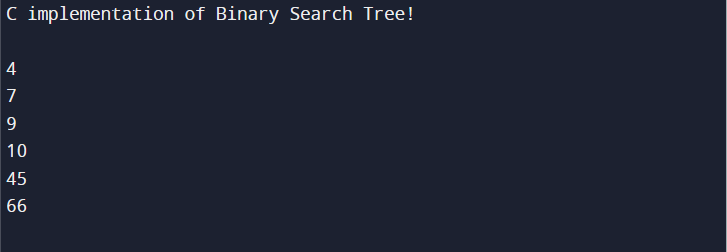
Заключение
Деревья часто используются для хранения данных в нелинейной форме. Бинарные деревья - это типы деревьев, в которых каждый узел (родительский) имеет два потомка: левый дочерний элемент и правый дочерний элемент. А бинарное дерево универсальный метод передачи и хранения данных. Он более эффективен по сравнению с Linked-List в C. В приведенной выше статье мы рассмотрели концепцию Бинарное дерево с поэтапной реализацией Бинарное дерево поиска в С.